| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- #패스트캠퍼스 #패스트캠퍼스부트캠프 #데이터분석 #데이터분석부트캠프 #BDA11기 #국비지원 #패스트캠퍼스국비지원
- #데이터분석가 #DataAnalyst #SQL #프로젝트 #취준생
- 패스트캠퍼스 #패스트캠퍼스부트캠프 #데이터분석 #데이터분석부트캠프 #BDA11기 #국비지원 #패스트캠퍼스국비지원
- #패스트캠퍼스 #패스트캠퍼스부트캠프 #데이터분석 #데이터분석부트캠프 #패스트캠퍼스데이터분석부트캠프 #BDA11기 #국비지원 #패스트캠퍼스국비지원 '데이터분석 부트
- #패스트캠퍼스 #패스트캠퍼스부트캠프 #데이터분석 #데이터분석부트캠프 #패스트캠퍼스데이터분석부트캠프 #BDA11기 #국비지원 #패스트캠퍼스국비지원
- Today
- Total
STUDY-LOG
[패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 2주차 본문
📌EXCEL로 하는 데이터분석 / 기초수학 &통계
🙋🏻♀️지난주에 이어 이번주도 Excel을 활용해 데이터를 분석해보는 시간이었다.
수많은 엑셀 함수들 중 데이터 분석에 유용하게 쓰이는 함수들과 분석한 데이터를 내가 표현하고자하는데로 나타낼 수 있는 다양한 시각화 방법을 배웠고, 또한 데이터 분석에 빠질 수 없는 통계학에 관하여 deep하진 않을정도(?)로 배워보았다.
+) 부트캠프 시작한지 2주차인데 Peer Session도 가져보았고 한 챕터를 마무리하는 너낌으로 퀴즈(객관식 15문제로 이루어진 퀴즈는 가벼운 마음으로 봤지만 긴장되었고 걱정했지만 다 맞아서 놀랬다는..ㅎ)도 봐서 그런지 알찬 5일이었다🙃
< 탐색적 데이터 분석(EDA, Exploratory Data Analysis) >
: 주어진 자료만 가지고도 충분한 정보를 찾을 수 있도록 하는 자료 분석 방법
✔ 결측치 (Missing Value)
✔ 이상치 (Outlier)
✔ 상관분석
✔ 결측치 (Missing Value) : 데이터에 값이 없는 것
| NA | Not Available, 유효하지 않는 |
| NaN | Not a Number, 숫자가 아닌 |
| Null | 아무것도 존재하지 않음을 의미 |
| 빈칸 | 데이터가 입력되지 않음 ⇒ 대부분의 엑셀의 경우 |
>> 결측치 처리
- 제거: 결측치가 발생한 행, 열을 삭제하는 가장 쉽고, 단순한 방식
- 치환: 결측치를 적당한 방법으로 대체하는 것
- 모델 기반 처리: 결측치를 예측하는 새로운 모델을 구성해, 결측치를 해워 나가는 방식
✔ 이상치(Outlier) : 특정 지정된 그룹에 분류되지 못하는 값으로, 정상군의 상한과 하한의 범위를 벗어나 있거나 패턴에서 벗어난 수치
⇒ 일반적으로 -3σ (표준편차) 미만, +3σ 초과인 값을 이상치로 판정

💡 어떤 데이터를 관측했을 때(실험했을 때), 평균을 기준으로 평균에 가장 가까운 데이터가 나올 확률이 높은 OR 평균에서 멀어질수록 극단적인 값이 나올 확률이 적은 분포가 정규분포
>> 이상치는 반드시 제거해야 하는가
⇒ 이상치는 분석 결과의 질을 떨어뜨리거나 왜곡시킬 수 있으므로 제거하거나 다른 값으로 대체하는 경우가 많지만, 상황에 따라서는 제거하지 않고 분석해야 하는 경우도 있을 수 있음
>> Z-Score
: 자료가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 나타내는 지표

>>>Z-Score의 특징
- Z-Score > 0 : 자료값이 평균보다 높음
- Z-Score < 0 : 자료 값이 평균보다 낮음
- 0에 가까운 Z-Score은 자료 값이 평균과 비슷함
- 일반적으로 Z-Score ≥ 3 이거나 Z-Score ≤ -3이면 이상치로 판단 (절대적인 기준X)
>> 사분위수 (Quartile)
- 제1사분위수(1Q, 25%): ( (N-1) X 0.25 ) + 1
- 제2사분위수(2Q, 중앙값)
- 제3사분위수(3Q, 75%): ( (N-1) X 0.75 ) + 1
- IQR (Interquartile Range) ⇒ IQR = 3Q - 1Q
- 보통 1Q지점에서 아래로 1.5IQR 떨어져 있거나, 3Q 지점에서 위로 1.5IQR 더 떨어져 있는 지점
- 이상치 < 1Q -1.5IQR, 3Q +1.5IQR < 이상치
- Box Plot

✔ 상관분석 : 두 변수가 어떤 선형적 관계를 갖고 있는지를 분석하는 방법
>> 상관관계
: 한쪽이 증가하면 다른 쪽도 증가하거나 반대로 감소되는 경향을 인정하는 두 양(量) 사이의 통계적 관계
⇒ 상관 계수를 통해 파악
>> 상관계수 (Pearson Correlation Coefficient)
- 상관 계수 r은 두 변수 사이의 상관성을 나타내며 일반적으로 피어슨(Pearson) 상관 계수를 사용
- -1 ≤ r ≤ 1
- 상관 계수가 1에 가까울 수록 양의 상관 관계(정비례), 일반적으로 +0.7 이상이면 강한 양의 상관 관계
- 상관 계수가 -1에 가까울수록 음의 상관 관계(반비례), 일반적으로 -0.7 이하이면 강한 음의 상관 관계
- EDA에서 상관 분석의 역할
- 인과 관계가 있을 것으로 예상되는 변수들을 선별해 분석의 우선순위를 정할 수 있음 → 시간과 비용의 효율성 증대
- but, 강한 상관 관계를 가지고 있다해서 두 변수가 반드시 인과 관계를 가지는 것은 아님
< 데이터 전처리 >
: 데이터의 분석 목적과 방법에 맞게 데이터를 가공 또는 처리하는 과정
✔ 데이터 전처리 함수
✔ 데이터 전처리 기능
✔ 데이터 전처리 함수
>> IF 함수

>> VLOOKUP, MATCH, IDEX, COUNT, SUMIF, FIND, LEFT, RIGHT, MID 함수
지난 포스팅에 다뤄봤으므로,, 👉참고하기
✔ 데이터 전처리 기능
>> 텍스트 나누기
⇒ ⇒ [데이터]탭 → [텍스트 나누기] → [구분 기호로 분리됨] → [기타] 체크 → “-” 입력 → [마침]
>> 중복 항목 제거
⇒ ⇒ [데이터]탭 → [중복된 항목 제거] → 중복 값을 제거할 기준 열 선택 → [확인]
>> 필터와 고급필터
⇒ :필터는 필터링(필요한 데이터만 선택 or 필요하지 않은 데이터 제외) 기능과 데이터 정렬(오름차순, 내림차순) 기능을 가지고 있음
⇒ ⇒ 필터 단축키: [Alt] + [D] + [F] + [F], [Alt] + [A] + [T], [Ctrl] + [Shift] + [L]
⇒ ⇒ 고급필터: 조건을 한 행에 쓰면 AND 조건, 여러 행에 쓰면 OR 조건
>> 데이터 유효성 검사
⇒ : 특정 셀이나 범위, 상황에 따라 유요하다고 인정하는 데이터만 입력하는 기능
⇒ ⇒ 조건설정: 셀/범위 지정 → [데이터] → [데이터 유효성 검사] → [제한 대상], [제한 방법] 지정
< 통계학 (Statistics) >
- 산술적 방법을 기초로 하여, 주로 다량의 데이터를 관찰하고 정리 및 분석하는 방법을 연구하는 수학의 한 분야
- 연구 목적에 필요한 자료 및 정보를 최적한 방법으로 수집하고, 수집한 자료를 과학적이고 논리적인 이론에 의하여 정리 분석하는 학문
- 통계학은 관심 또는 연구의 대상이 되는 모집단(population)으로 부터 자료를 수집, 정리, 요약을 하고 표본(수집한 자료, sample) 정보로부터 자료를 추출했던 대상 전체인 모집단에 대한 최적의 의사 결정을 내릴 수 있도록 정확한 정보를 제공하는 방법론을 연구하는 학문
✔ 기술통계학
✔ 추론통계학
✔ 통계적 데이터 분석
✔ 기술 통계학 (Descriptive Statistics)
- 요약 통계량, 그래프, 표 등을 이용해 데이터를 정리, 요약하여 데이터의 전반적인 특성을 파악하는 방법
- 표, 그래프 등을 활용해 데이터를 시각적으로 표현하고 통계량 등으로 수치를 요약
- 데이터의 특징을 파악하는 관점 -- EDA 단계에서 주요하게 사용됨
✔ 추론 통계학 (Inference Statistics)
- 데이터가 모집단으로부터 나왔다는 가정하에 모집단으로부터 추출된 표본을 사용하여 모집단의 특성을 파악하는 방법
- 전체 모집단을 조사할 수 없을 때 유용
- 점 추정, 구간 추정을 하거나 가설을 검정함
>> 모집단
: 아직 가지고 있지 않은 모르는 데이터를 포함한 모든 데이터 = 관심의 대상이 되는 집단
>> 표본
: 모집단의 전체 데이터를 분석하기 위해 수집된 일부 데이터
>> 가설검정 (Hypothesis Testing)
: 통계적 추론으로, 모집단 실제의 값이 얼마가 된다는 주장과 관련해 표본의 정보를 사용해 가설의 합당성 여부를 판단하는 과정
- 귀무 가설(H0, null hypothesis): 기본적으로 참으로 추정되며 처음부터 버릴 것으로 예상하는 가설 (차이가 없거나, 의미 있는 차이가 없는 경우)
- 대립 가설(H1, 연구 가설): 귀무 가설에 대립하는 명제, 보통 독립 변수와 종속 변수 사이에 어떤 특정한 관련이 있다는 결과가 도출됨, 귀무가설을 기각하는 반증의 과정을 거쳐 참이라고 받아들여질 수 있음
>> p-value (유의 확률)
: 가설 검정의 기준, 귀무가설(H0)이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 ‘같거나 더 극단적인’ 통계치가 관측될 확률
- p-value는 관계나 집단들 사이에 차이가 생겨나는 것이 우연한 것인지, 변수에 의한 것인지 여부를 밝히는 것
- 하지만, 효과나 변화의 정도, 또는 관계의 강도나 크기 등을 설명하는 것은 아님
>> t-test
: 두 집단(또는 한 집단의 전,후)의 평균에 통계적으로 유의미한 차이가 있는지를 검정
- 시행단계: 변수(집단) 선택 ⇒ F-test ⇒ t-test ⇒ 결과 해석
- t-test H0: 두 집단의 평균에 유의미한 차이가 없다 (p > 유의수준)
- t-test H1: 두 집단의 평균에 유의미한 차이가 있다 (p < 유의수준)
>>> F-test
: 두 집단의 분산에 통계적으로 유의미한 차이가 있는지를 검정
- F-test H0: 두 집단의 분산에 유의미한 차이가 없다 (p > 유의수준)
- F-test H1: 두 집단의 분산에 유의미한 차이가 있다 (p < 유의수준)
- *유의수준 = 0.05
✔ 통계적 데이터 분석
>> 회귀분석 (Regression Analysis)
: 두 개 이상의 연속형 변수(수치)인 종속 변수와독립 변수 간의 관계를 파악하여 우리가 알고 싶은 값을 예측하는 것이 목적인 분석

- 종속변수: 우리가 알고 싶은 값
- 독립변수: 우리가 알고 있는 값, 종속변수를 설명하기 위한 변수
- 종류:
| 회귀분석 | 선형회귀분석 함수식이 선형함수 식 |
단순선형회귀분석 독립변수(x)가 1개 |
| 다중선형회귀분석 독립변수(x)가 여러개 |
||
| 비선형회귀분석 함수식이 선형함수 식 X |
>>> 단순선형회귀 (Simple Linear Regression)
: 독립변수(x)가 변할 때, 종속변수(y)값이 어떻게 변하는지를 가장 잘 설명해주는 직선을 찾아 그 직선이 x와 y의 관계를 얼마나 설명하고 있는지 분석하는 방법 ⇒ y와 x사이의 1차 방정식
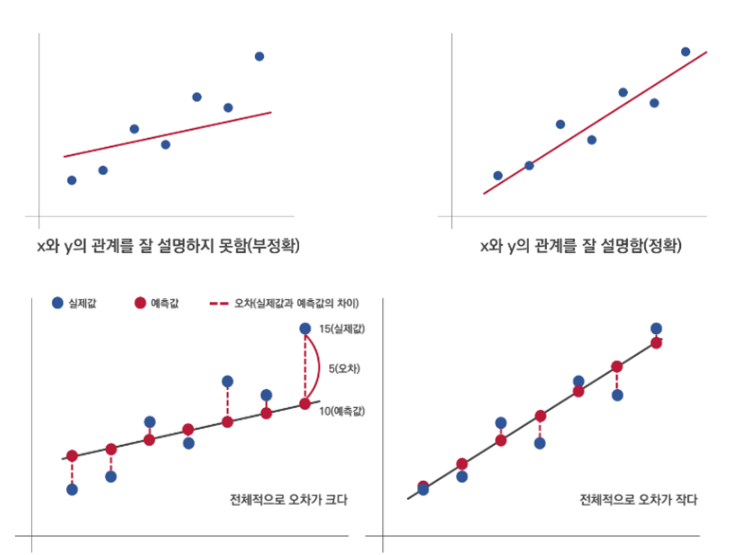
- 결정계수: 0~1의 값을 가지며 1에 가까울수록 회귀 모형이 실제 값을 잘 설명
- F값: 0.05 > F 이면 회귀 모형이 유의미하므로 사용 가능함
- y절편(b의 값)과 x의 계수(a, 기울기)
- 실습

>>> 다중선형회귀 (Multiple Linear Regression)
: 독립 변수가 x_1, x_2, x_3 등으로 2개 이상일 때 독립 변수들과 종속 변수 간의 관계를 파악하는 분석
- 조정된 결정 계수: 0~1의 값을 가지며 1에 가까울수록 회귀 모형이 실제 값을 잘 설명
- F값: 0.05 > F 이면 회귀 모형이 유의미하므로 사용 가능함
- y절편(b의 값)과 각 독립변수의 p-value
- 실습

>> 시계열 분석 (Time Series Analysis)
: 시간의 흐름에 따라 발생된 데이터를 분석하는 기법
- 시계열 데이터의 유형: 정상성을 가지고 있는 정상 시계열 데이터와 정상성을 가지고 있지 않은 비정상 시계열 데이터로 구분
- 정상성: 추세나 계절성을 가지고 있지 않으며, 관측된 시간에 무관한 성질
- 정상 시계열: 규칙적인 패턴을 가진 시계열 데이터
- 비정상 시계열: 불규칙적인 패턴을 가진 데이터
- 대부분의 시계열 데이터는 비정상 시계열 데이터
- 비정상 시계열 데이터인 상태로는 분석이 어렵기 때문에 차분이나 다른 방법을 활용해 비정상 시계열 데이터를 정상 시계열 데이터로 변환해 분석
- 지수 평활법 (Exponential Smoothing)
- 현재 시점에 가까운 시계열 자료에 큰 가중치를 주고, 과거 시계열 데이터일수록 작은 가중치를 주어 미래 시계열 데이터를 예측하는 기법
- 단순 지수 평활법 (Simple Exponential Smoothing) ⇒ 미래 예측 값 = 과거의 실제 값 x α + 과거의 예측 값 x (1 - α)
- 엑셀에서 사용할 수 있는 지수 평활법 관련 예측 함수: FORECAST.ETS(target_date, values, timeline, [seasonality], [data_completion], [aggregation]) ⇒ 비교적 뚜렷한 계절성이 있는 데이터 예측에 사용
'데이터분석 부트캠프 > 학습일지' 카테고리의 다른 글
| [패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 8-10주차 (0) | 2023.12.29 |
|---|---|
| [패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 6-7주차 (0) | 2023.12.07 |
| [패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 4주차 (0) | 2023.11.17 |
| [패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 3주차 (0) | 2023.11.06 |
| [패스트 캠퍼스] 데이터 분석 부트캠프(BDA) 11기 1주차 (0) | 2023.10.26 |




